AC自动机以trie为基础，结合了kmp的next数组思想而创造出来的一种数据结构，用来解决多模式串匹配问题

问题背景

P3808 【模板】AC自动机（简单版）

给定n个模式串（$n<=1e6$），一个主串s（$s<=1e6$），问主串中包含多少个这些之中的模式串？

AC自动机

传统做法，利用KMP，O(n)遍历每一个模式串，O(n)匹配是否包含此模式串，复杂度O(n2)

利用AC自动机，先把所有的模式串插入到trie中，接下来预处理一个fail数组，fail[i]表示i节点失配后该去找哪个节点（类似next数组），fail数组的真正含义是当前正在匹配的模式串的后缀和其他所有模式串的前缀可以匹配最大长度的那个模式串，有点绕。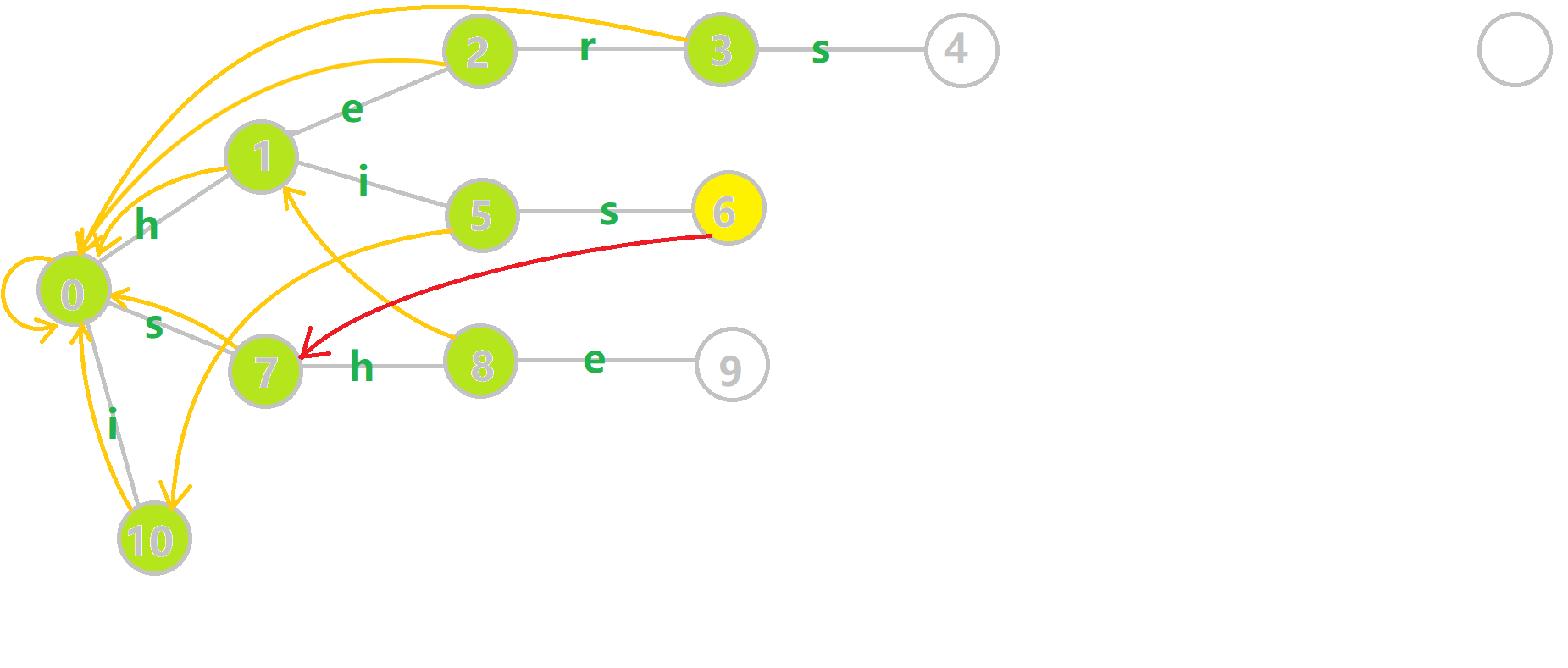

这张图中的6号节点的fail指针指向7号节点，因为6号节点的后缀s和7号节点的前缀s相同，且匹配长度最大，所以fail[6]=7。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
queue<int> q;
void build(){
    //这里把根节点的儿子节点入队，因为如果只把根节点入队的话会导致根节点失配指针指向自己，那么第一次bfs求儿子节点的fail指针时，儿子的fail也会指向自己
    for(int i=0;i<26;i++){
        if(tr[0][i]) q.push(tr[0][i]);
    }
    //利用bfs进行构建
    while(!q.empty()){
        int u=q.front();
        q.pop();
        for(int i=0;i<26;i++){
            if(tr[u][i]){
                fail[tr[u][i]]=tr[fail[u]][i];
                q.push(tr[u][i]);
            }
            else tr[u][i]=tr[fail[u]][i];	//压缩路径
        }
    }
    return ;
}

image-20210820104813489

预处理出fail数组后即可进行主串匹配，需要注意的是每一个字符都要当作失配字符进行一次不断向fail数组跳跃的过程，过程中记录出现的模式串。

例如

t1: ash

t2: sh

S: ash

匹配时可以直接匹配到ash，但是sh是藏在ash中的，所以在匹配ash的过程中时刻需要看看有没有其他的模式串的前缀和当前字符串的后缀匹配成功的，sh的前缀就和ash的后缀匹配上了，然后发现这正是fail数组的意义，所以每次跳跃到fail[i]即可。

1
2
3
4
5
6
7
8
9
10
11
12
int query(string s){
    int len=s.size(),u=0,ret=0;
    for(int i=0;i<len;i++){
        u=tr[u][s[i]-'a'];
        for(int j=u;j && num[j]!=-1;j=fail[j]){	
            //每一个字符都当成失配字符算一遍匹配模式串数量
            ret+=num[j];
            num[j]=-1;	//一个模式串被计算过了就要标记一下
        }
    }
    return ret;
}

AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include <bits/stdc++.h>
//#pragma G++ optimize(2)
//#pragma G++ optimize(3,"Ofast","inline")
#define endl '\n'
#define debug freopen("in.txt","r",stdin); freopen("out.txt","w",stdout)
#define ios ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
const int MAXN=1e6-100;
const int MOD=1e9+7;
const int INF=0x3f3f3f3f;
const int SUB=-0x3f3f3f3f;
const double eps=1e-4;
const double E=exp(1);
const double pi=acos(-1);
string s;
int n;
struct AC{
	int tr[MAXN][27],num[MAXN],fail[MAXN];	//tr: 字典树数组、num:记录模式串数量、失配跳转指针
	int tot;	//点编号
	void insert(string s){	//插入模式串，构建字典树
		int p=0,len=s.size();
		for(int i=0;i<len;i++){
			if(!tr[p][s[i]-'a']) tr[p][s[i]-'a']=++tot;
			p=tr[p][s[i]-'a'];
		}
		num[p]++;	//数量加一
		return ;
	}
	queue<int> q;
	void build(){
		for(int i=0;i<26;i++){
			if(tr[0][i]) q.push(tr[0][i]);
		}
		while(!q.empty()){
			int u=q.front();
			q.pop();
			for(int i=0;i<26;i++){
				if(tr[u][i]){
					fail[tr[u][i]]=tr[fail[u]][i];
					q.push(tr[u][i]);
				}
				else tr[u][i]=tr[fail[u]][i];	//压缩路径
			}
		}
		return ;
	}
	int query(string s){
		int len=s.size(),u=0,ret=0;
		for(int i=0;i<len;i++){
			u=tr[u][s[i]-'a'];
			for(int j=u;j && num[j]!=-1;j=fail[j]){	
			//每一个字符都当成失配字符算一遍匹配模式串数量
				ret+=num[j];
				num[j]=-1;	//一个模式串被计算过了就要标记一下
			}
		}
		return ret;
	}
};
AC tree;
int main(){
	// debug;
	ios;
	cin>>n;
	for(int i=0;i<n;i++){
		cin>>s;
		tree.insert(s);
	}
	tree.build();
	cin>>s;
	cout<<tree.query(s)<<endl;
	return 0;
}

/*

*/