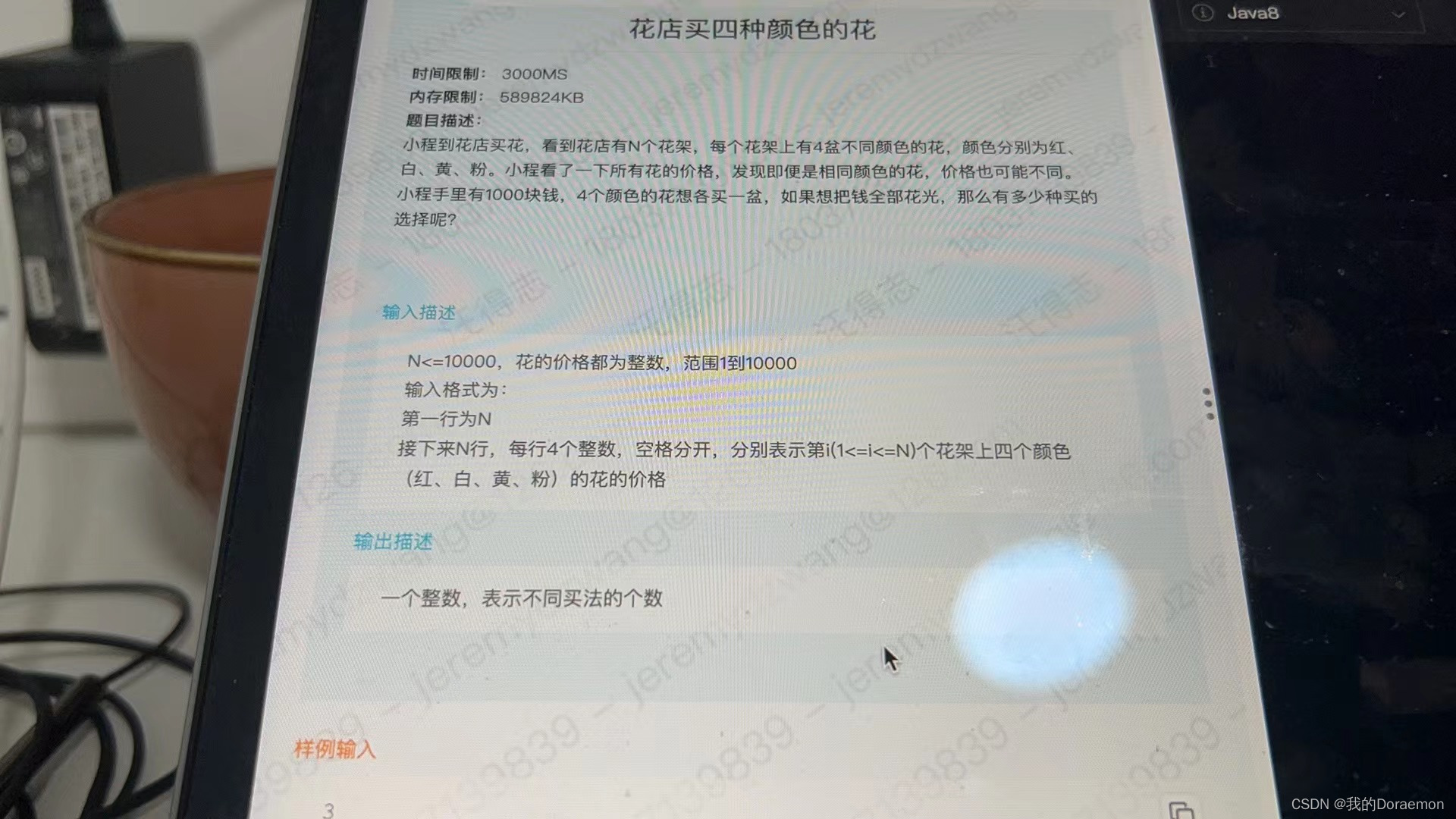
四种类型的物品，每一种类型物品数量都是n，先要从每种类型的物品中挑选一件，使得最后花费总和等于1000 暴力做法10000^4 看到花费总和是1000，很小且固定的数字，肯定有玄机，从这里想应该是用dp，不难想到用dp[i][j]表示前i种类型的物品花费为j的方案数量，思考转移方程： dp[i][j] = dp[i-1][j-A] * js[i][A]，js[i][A]表示i类型的物件花销为A的方案数量，如此只需要枚举j和A，它们的范围就是1000以内
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
| #include <iostream>
#include <vector>
#define ios ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
using namespace std;
int dp[5][1100], js[5][11000];
int n;
vector<int> ve[5];
int main() {
ios;
cin >> n;
for(int i = 1; i <= n; i ++) {
int a, b , c, d;
cin >> a >> b >> c >> d;
ve[1].push_back(a);
ve[2].push_back(b);
ve[3].push_back(c);
ve[4].push_back(d);
}
for(int i = 1; i <= 4; i++) {
for(int j = 0; j < ve[i].size(); j++) {
js[i][ve[i][j]] ++;
}
}
for(auto p : ve[1]) {
dp[1][p] ++;
}
for(int i = 2; i <= 4; i++) {
for(int j = 1; j <= 1000; j++) {
if(js[i][j]) {
for(int k = j; k <= 1000; k++) {
dp[i][k] += dp[i-1][k-j] * js[i][j];
}
}
}
}
cout << dp[4][1000];
return 0;
}
|
wechat
alipay
