数学期望

期望: 结果乘以结果出现的概率

$E(X+Y)=E(X)+E(Y)$

$E(XY)=E(X)E(Y)——(X和Y相互独立)$

问题一

描述

投硬币，连续出现K次正面的投掷次数期望值。

解法

假设已经连续抛出$n-1$次正面，需要$T{n−1}$次。想得到$n$次正面，则再进行一次投掷$Tn=T{n−1}+1+?$

若硬币为正面则游戏结束，还需要抛0次$Tn=T_{n−1}+1+0.5∗0+?$）

如果硬币为反面，则游戏重来，还需要投掷$0.5∗Tn$次，递推公式如下所示：

$Tn=T_{n−1}+1+0.5∗0+0.5∗Tn$

求出通项公式:

$Tn=2^{n+1}+2$

问题二

题目链接

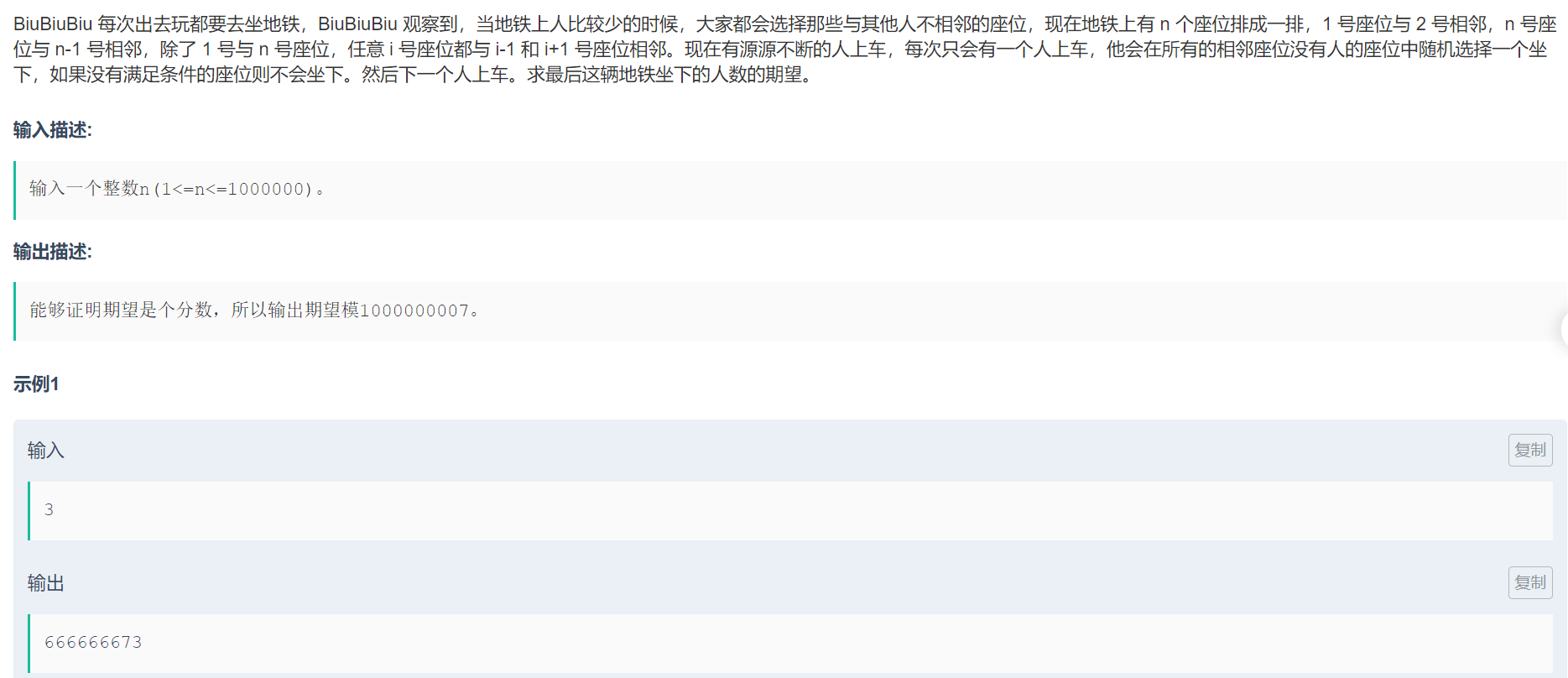
设dp[i]表示i个座位最后坐满人的情况，那么对于n个座位而言，第一个人上车就有n个选择，坐在第一个位置，剩下的就是dp[n-2]，坐在第二个位置，剩下的就是$dp[0]+dp[n-3]$，坐在第三个位置，剩下的就是$dp[1]+dp[n-4]$，以此类推…

求个和，就是$2*sum[n-2]$，sum[n-2]表示前n-2项的前缀和(dp[0]=0)

还要把第一个人加上，因为有n个选择，所以加n，每一个选择有$1/n$的概率，所以最后除以n

$dp[i]=(i+2*cnt)/n$

#include <bits/stdc++.h>
#define endl '\n'
#define ios ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
using namespace std;
typedef long long ll;
const int N=1000002;
const int mod=1000000007;
ll dp[N];
ll ksm(ll a,ll b){
	ll res=1;
	while(b){
		if(b&1) res=res*a%mod;
		a=a*a%mod;
		b>>=1; 
	}
	return res;
}
ll inv(int x){
	return ksm(x,mod-2);
}
int main()
{
	ios;
	dp[1]=1; dp[2]=1;
	ll cnt=1;
	int n;
	cin>>n;
	for(int i=3;i<=n;i++){
		dp[i]=(2*cnt%mod+i)*inv(i)%mod;
		cnt=(cnt+dp[i-1])%mod;
	}
	cout<<dp[n]<<endl;
	return 0;
}

问题三

描述

三个骰子，给出每个骰子的面数，求随机摇出的三个数字和出现次数最多的是什么？如果有多个和出现次数一样，输出最小的。

解法

大犇题解

#include <bits/stdc++.h>
using namespace std;
int a[5];
int main()
{
	for(int i=1;i<=3;i++) cin>>a[i];
	sort(a+1,a+1+3);
	if(a[2]<=(a[3]-a[1]+1)) cout<<1+a[1]+a[2]<<endl;
	else cout<<1+a[3]+(a[2]-(a[3]-a[1]+1))/2+1<<endl;
	return 0;
}