扩展KMP

解决的问题： 求解母串以i位置开始的后缀子串与模式串的最大公共前缀

时复： O(母串长度+模式串长度)

引入两个概念，extend[]数组表示以母串i位置开始的后缀子串与模式串的最大公共前缀，next[]数组表示模式串以i位置开始的后缀子串与模式串的最大公共前缀，一个是模式串与母串，一个是模式串与模式串

与KMP类似，都采用了利用之前已经得到的信息来优化当前的时间

大致过程

记一个po表示起始位置，求解extend数组需要先求出next数组，而求解next数组的过程和求extend过程一致，只不过是把模式串当作母串

img

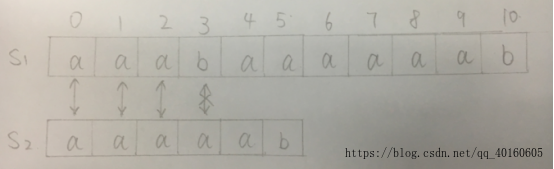
(1) 第一步，我们先对原串S1和模式串S2进行逐一匹配，直到发生不配对的情况。我们可以看到，S1[0]=S2[0],S1[1]=S2[1],S1[2]=S2[2],S1[3] ≠S2[3],此时匹配失败，第一步结束，我们得到S1[0,2]=S2[0,2],即extend[0]=3;

(2) Extend[0]的计算如第一步所示，那么extend[1]的计算是否也要从原串S1的1位置，模式串的0位置开始进行逐一匹配呢？扩展KMP优化的便是这个过程。从extend[0]=3的结果中，我们可以知道，S1[0,2]=S2[0,2],那么S1[1.2]=S2[1,2]。因为next[1]=4,所以S2[1,4]=S2[0,3],即S2[1,2]=S[0,1],可以得出S1[1,2]=S2[1,2]=S2[0,1],然后我们继续匹配，S1[3] ≠S2[3],匹配失败，extend[1]=2;

(3) 因为extend[1]=2,则S1[1,2]=S2[0,1],所以S1[2,2]=S2[0,0],因为next[0]=5,所以S1[0,5]=S2[0,5],所以S2[0,0]=S2[0,0],又回到S1[2,2]=S2[0,0],继续匹配下一位，因为S1[3] ≠S2[1],所以下一位匹配失败，extend[2]=1;

(4) 到计算原串S1的3号位置（在之前的步骤中能匹配到的最远的位置+1,即发生匹配失败的位置），这种情况下，我们会回到步骤（1）的方式，从原串S1的3号位置开始和模式串的0号位置开始，进行逐一匹配，直到匹配失败，此时的extend[]值即为它的匹配长度。因为S1[3] ≠S2[0],匹配失败，匹配长度为0，即extend[3]=0;

(5) 计算S1的4号位置extend[]。由于原串S1的4号位置也是未匹配过的，我们也是回到步骤（1）的方式，从原串S1的4号位置开始和模式串S2的0号位置开始进行逐一匹配，可以看到，S1[4]=S2[0],S1[5]=S2[1],S1[6]=S2[2],S1[7]=S2[3],S1[8]=S2[4],S1[9] ≠S2[5],此时原串S1的9号位置发生匹配失败，最多能匹配到原串S1的8号位置，即S1[4,8]=S2[0,4],匹配长度为5，即extend[4]=5;

(6) 计算S1的5号位置extend[].由于原串S1的5号位置是匹配过的（在步骤（5）中匹配了），我们从extend[4]=5得出，S1[4,8]=S2[0,4],即S1[5,8]=S2[1,4],和步骤（2）的计算方式类似，我们从next[1]=4可知，S2[0,3]=S2[1,4],即S1[5,8]=S2[0,3],然后我们继续匹配原串S1的9号位置和S2的4号位置，S1[9]=S2[4],继续匹配，S1[10]=S2[5],此时原串S1的所有字符皆匹配完毕，皆大欢喜，则S1[5,10]=S2[0,5],extend[5]=6;

(7) 从原串S1的6号位置到10号位置的extend[]的计算，与原串S1的1号位置到3号位置的计算基本相同。S1[6,10]=S2[1,5],因为next[1]=4，所以S2[1,4]=S[0,3],所以S1[6,9]=S2[0,3],此时不在需要判断匹配下一位的字符了，直接extend[6]=4;(具体原因在后面的分析总结中有说明)

(8) S1[7,10]=S2[2,5],因为next[3]=2,所以S2[3,4]=S2[0,1],所以S1[8,9]=S2[0,1],匹配长度为2，即extend[7]=3;

(9) S1[8,10]=S2[3,5],因为next[3]=2,所以S2[3,4]=S2[0,1],所以S1[8,9]=S2[0,1],匹配长度为2，即extend[8]=2;

(10) S1[9,10]=S2[4,5],因为next[4]=1,所以S2[4,5]=S2[0,0],所以S1[9,9]=S2[0,0],匹配长度为1，即extend[9]=1;

(11) S1[10,10]=S2[5,5],因为next[5]=0,所以匹配长度为0，即extend[10]=0;

至此，所有的匹配已经结束，相信，如果你仔细的看了上述的例子，已经对扩展KMP有了一定的了解了，它的计算过程中，主要是步骤一和步骤二的计算过程。下面我们对这两个过程归纳一下：

img

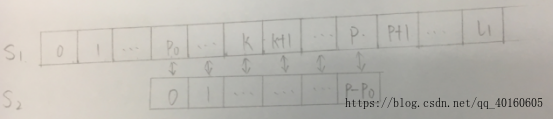
我们可以得出，len=next[k+1-Po],S2[0,len-1]=S2[k+1-Po,k+Po+len],所以S1[k+1,k+len]=S2[k+1-Po,k+Po+len]=S2[0,len-1],即extend[k+1]=len;

那么会不会出现S1[k+len+1]=S2[len]的情况呢？答案是否定的

假如S1[k+len+1]=S2[len],则S1[k+1,k+len+1]=S2[0,len]

因为k+len<P,所以k+len+1<=P

所以S1[k+1,k+len+1]=S2[k+1-Po,k+Po+len+1]=S2[0,len]

此时，next[k+1-Po]=len+1与原假设不符合，所以此时S1[k+len+1]≠S2[len],不需要再次判断。

（2）当（k+1）+len-1=k+len>=P时，即以下情况：

img

我们可以看出，由S1[Po,P]=S2[0,P-Po]可得出S1[k+1,P]=S2[k+1-Po,P-po]，len=next[k+1-Po],所以S2[0,len-1]=S2[k+1-Po,k+len+Po]

所以S1[k+1,p]=S2[0,P-k-1]

由于大于P的位置我们还未进行匹配，所以从原串S1的P+1位置开始和模式串的P-k位置开始进行逐一匹配，直到匹配失败，并更新相应的Po位置和最远匹配位置P,此时extend[k+1]=P-k+后来逐一匹配的匹配长度。

其实，next[]数组的计算过程与extend[]的计算过程基本一致，可以看成是原串S2和模式串S2的扩展KMP进行计算，每次计算extend[k+1]时，next[i](0<=i<=k)已经算出来了，算出extend[k+1]的时候，意味着next[k+1]=extend[k+1]也计算出来了。

时间复杂度分析

通过上面的算法可知，我们原串S1的每一个字符串只会进行一次匹配，extend[k+1]的计算可以通过之前extendi\的值得出，由于需要用相同的方法对模式串S2进行一次预处理，所以扩展KMP的时间复杂度为O(l1+l2),其中，l1为原串S1的长度，l2为模式串S2的长度。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
void getnext(string T){
	int len=T.size();
	nex[0]=len;
	int p=0;
	while(p+1<len && T[p]==T[p+1]) p++;  //这里注意把边界写在前面
	nex[1]=p;
	int po=1;
	for(int i=2;i<len;i++){
		if(i+nex[i-po]<po+nex[po]) nex[i]=nex[i-po];  //第一种情况，直接得到答案
		else{
			int j=po+nex[po]-i;  
			if(j<0) j=0;  //超出已匹配的字符串长度，需要重新匹配
			while(i+j<len && T[i+j]==T[j]) j++;
			nex[i]=j;
			po=i;  //长度超出，更新起始位置
		}
	}
}
void extmp(string S,string T){
	int len1=S.size(), len2=T.size();
	getnext(T);
	int p=0;
	while(p<len1 && p<len2 && S[p]==T[p]) p++;  //边界写到前面
	ext[0]=p;
	int po=0;
	for(int i=1;i<len1;i++){
		if(i+nex[i-po]<po+ext[po]) ext[i]=nex[i-po];
		else{
			int j=po+ext[po]-i;
			if(j<0) j=0;
			while(i+j<len1 && j<len2 && T[j]==S[i+j]) j++;
			ext[i]=j;
			po=i;
		}
	}
}

武辰延的字符串

题目

image-20210407203042725

可以用扩展KMP来做，将s2当作母串，对于s1和s1的公共前缀子串，每一个位置的extend值累加起来就是答案

code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include<bits/stdc++.h>
#define ios ios::sync_with_stdio(0); cin.tie(0); cout.tie(0)
using namespace std;
string S,T;
long long ext[110000],nex[110000];
void getnext(string T){
	int len=T.size();
	nex[0]=len;
	int p=0;
	while(p+1<len && T[p]==T[p+1]) p++;
	nex[1]=p;
	int po=1;
	for(int i=2;i<len;i++){
		if(i+nex[i-po]<po+nex[po]) nex[i]=nex[i-po];
		else{
			int j=po+nex[po]-i;
			if(j<0) j=0;
			while(i+j<len && T[i+j]==T[j]) j++;
			nex[i]=j;
			po=i;
		}
	}
}
void extmp(string S,string T){
	int len1=S.size(), len2=T.size();
	getnext(T);
	int p=0;
	while(p<len1 && p<len2 && S[p]==T[p]) p++;
	ext[0]=p;
	int po=0;
	for(int i=1;i<len1;i++){
		if(i+nex[i-po]<po+ext[po]) ext[i]=nex[i-po];
		else{
			int j=po+ext[po]-i;
			if(j<0) j=0;
			while(i+j<len1 && j<len2 && T[j]==S[i+j]) j++;
			ext[i]=j;
			po=i;
		}
	}
}
int main()
{
	ios;
	cin>>T>>S;
	extmp(S,T);
	long long len1=T.size(),len2=S.size(),ans=0;
	for(int i=0;i<len1;i++){
		if(i>=len2) break;
		if(T[i]!=S[i]) break;
		ans+=ext[i+1];
	}
	cout<<ans<<'\n';
	return 0;
 }