马拉车算法(Manacher)

:::success

解决的问题：

以O(n)时间求出一个字符串的最长回文子串长度

:::

算法流程

如果求最大回文子串，暴力做法是从一个点开始，每次向左和右同时延伸一个单位，比较是否相同，但是这种方式比较难受的是如果字符串长度是偶数，那么可能对称中心不在字符上，而在两个字符之间，如果还想使用上面的方法就必须让指针在字符之间停留一下，所以考虑在每一个字符之间以及开头结尾（开头结尾添加是要让添加字符后的答案和未添加时的答案有一个对应关系）都添加相同的未出现的字符，这里用”#”表示，这样一来aba就变成了#a#b#a#，这样一来无论原串的长度为奇或偶转化后的字符串长度永远是奇数(2*l+1)，这时会发现添加后的字符串找出来的最长回文子串长度永远等于原串的最长回文子串长度+1（无论原串长度为奇数或偶数），所以对改变后的字符串求解的答案-1就是答案。

引入Len数组表示一个字符向左或向右可延伸的最长回文长度，比如aba，那么Len[1]=2（ab）

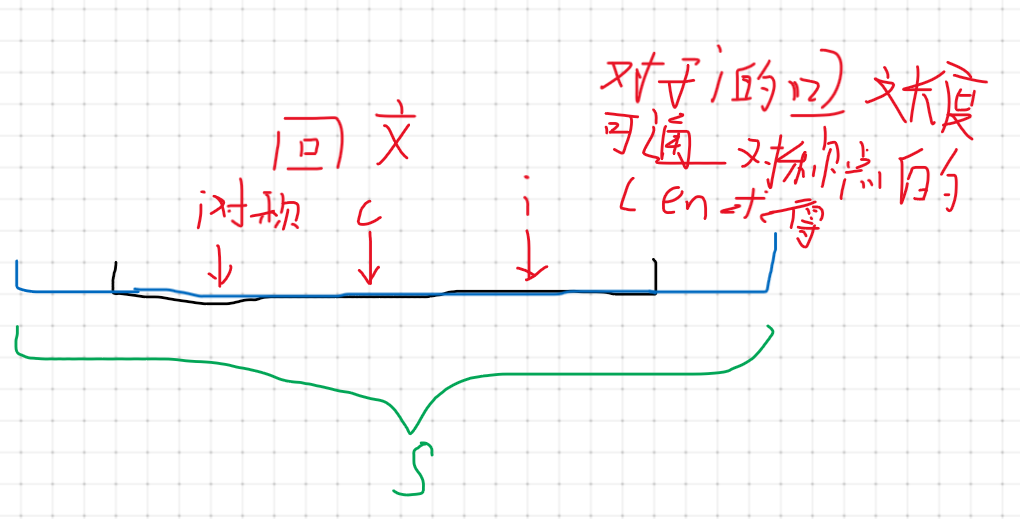
image-20210409161400175

当求Len[i]时Len[i_mirror]是已知的，又因为黑色区域都是回文的，所以Len[i]=min(Len[i_mirror],mx-i)，之所以要和mx-i取一个较小的是因为可能左边的Len比较大，而对于当前位置的i+Len[i]超过了mx就会造成答案错误，因为mx右面的都还没有匹配过

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
string process(string s){
	int len=s.size();
	string ret;
	ret+="^";  //开头加上当前字符中没有的字符，而且开头的字符不能和结尾的字符相同，这是因为不能增加可匹配的回文长度（会改变答案） 
	for(int i=0;i<len;i++){
		ret+="#";
		ret+=s[i];
	}
	ret+="#$";  //结尾加上和开头不一样的字符 
	return ret;
}
int manacher(string s){
	s=process(s);  //加上特殊字符，使得字符数量变成奇数 
	int c=0,mx=0,len=s.size(),sum=0;
	for(int i=1;i<len;i++){
		if(i<mx) Len[i]=min(mx-i,Len[2*c-i]);  //2*c-i就是关于c的对称点 ，之所以取min是因为可能左边的Leni比较大，
											  //这个点如果向右延伸这么长就超出mx了，而mx右面的位置都是没有匹配的，不确定是否可以组成回文 
		else Len[i]=1;  //如果当前位置已经超出最大的匹配范围了，就设置为1（当前字符就算一个回文） 
		while(s[i+Len[i]]==s[i-Len[i]]) Len[i]++;  //从当前点进行暴力匹配查看当前点可以延伸的最大长度 
		if(i+Len[i]>mx){  //如果超出了最大可延伸长度则更新 
			c=i;  //更新对称中心 
			mx=i+Len[i];  //更新最大延伸长度 
			sum=max(sum,Len[i]);  //更新答案 
		}
	}
	return sum-1;  //答案要减1，无论奇偶转换后的字符串求得的最大回文长度都是答案减1，可以手推一下，很简单的 
	//aba (#a#b#a#)
	//abba (#a#b#b#a#)
}

延伸求最大回文子串长什么样

既然有了最大回文子串的长度，也可以计算出匹配到最大长度时的对称中心下标，那么只要找到原串和处理过的字符串的下标对应关系就可以求出max回文子串长啥样了，经过模拟发现j=2(i+1)(j:处理过的下标)，i-Len[i]+2是匹配到的最长回文子串的开头字符的下标，所以可以求得最大回文子串

1
2
3
4
5
6
//修改此处即可
if(Len[i]>sum){
    sum=Len[i];
    st=(i-Len[i]+2)/2-1;
return bk.substr(st,sum-1);  //答案要减1，无论奇偶转换后的字符串求得的最大回文长度都是答案减1，可以手推一下，很简单的