遗传算法
基本概念
- 种群:群体的集合
- 位串:个体的表示形式。对应于遗传学中的染色体。
- 基因:位串上的一个元素,S=1011,则其中的1,0,1,1这4个元素分别称为基因。
- 编码:解空间中的解在遗传算法中的表示形式。从问题的解(solution)到基因型的映射称为编码,即把一个问题的可行解从其解空间转换到遗传算法的搜索空间的转换方法。
- 解码:遗传算法染色体向问题解的转换。
- 适应度:每个个体染色体和优秀染色体的基因序列差值大小
- 变异:0变1,1变0,概率小 (搜索与原来相差较小的解)
备注:常见的编码方法有二进制编码、格雷码编码、 浮点数编码、各参数级联编码、多参数交叉编码等。
二进制编码:即组成染色体的基因序列是由二进制数表示,具有编码解码简单易用,交叉变异易于程序实现等特点。
格雷编码:两个相邻的数用格雷码表示,其对应的码位只有一个不相同,从而可以提高算法的局部搜索能力。这是格雷码相比二进制码而言所具备的优势。
浮点数编码:是指将个体范围映射到对应浮点数区间范围,精度可以随浮点数区间大小而改变。
交叉:(搜索与原来相差较大的解)
单点交叉:选择一个交叉点,交叉交换
多点交叉:选择两个交叉点,交换中间的基因序列
均匀交叉:不选交叉点,0不交叉,子代1来自父代1,子代2来自父代2;1交叉,子代1来自父代2,子代2来自父代1
洗牌交叉:先打乱基因序列,然后选择交叉点交叉,目的是消除交叉点的选择对于结果的影响
选择:
1)轮盘赌:$p(xi)=\frac{f(x_i)}{\sum{i=1}^nf(x_i)}$,表示选择个体的概率,如果适应度函数值为0,则概率为0,就导致无法选择这个个体,违背了任何个体都有概率选择的原则,容易落入局部最优解
2)线性排序选择:
a)最差的选择概率:$p_{min}=\frac{2}{n(n+1)}$,
b)最好的选择概率:$p_{max}=\frac{2}{(n+1)}$,
c)中间的选择概率:$pi=p{min}+(p{max}-p{min})\frac{i-1}{n-1}\forall i\in{1,..,n}/{1,n}$
实战
以Max-cut problem问题为例,即将一个无向图切成2个部分(子图),从而使得2个子图之间的边数最多。
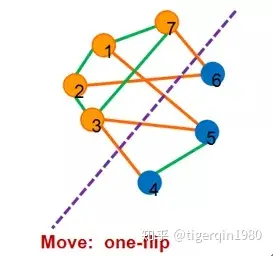
Step 1: 初始解
(1)设置种群的大小,编码染色体,初始种群:
设定种群的大小为10,编码位数为7位(因为有7个节点),初始人口:
S1=7(0001111),S2=5(0011010),S3=7(1110000),S4=7(1011011)
S5=7(0101100),S6=5(0111100),S7=3(1110011),S8=4(0011110),S9=6(0001101),S10=6(1101001);
其中,编码方式为:对无向图的每个节点进行编号,把无向图切成两个子图,划为子图1的用1表示,划为子图2的用0表示。
例如S1=7,表示把无向图切成两个子图,两个子图之间的边数为7,此时我们可以把编号为4,5,6,7的顶点划为子图1,把编号为1,2,3的顶点划为子图2,故可编码为0001111,但不唯一(因为两个子图之间的边数为7的切割方式并不唯一)。
(2)定义适应度函数:
$F(X)$计算两部分之间的边数
Step2:选择父代
(用轮盘赌方法从群体中随机选择两个父代)
S4=7(1011011)
S5=7(0101100)
Step3:杂交
对选取的父代进行杂交得到子代,其中杂交方法为若两个父代的同一节点在相同集合中,则保留;否则,对随机分配该节点至任意集合中。
交叉后: 子代=0011110(4)
Step4:变异
设定遗传概率,在0.05的概率下,将子代的某个节点从一个集合移动到另一个集合中。变异后:
子代=0010110(6)
Step5:群体更新
子代=0010110(6)
从S1=7(0001111),S2=5(0011010),S3=7(1110000),S4=7(1011011),
S5=7(0101100),S6=5(0111100),S7=3(1110011),S8=4(0011110),S9=6(0001101),S10=6(1101001)
中选取质量最差的个体出来,将这个用子代个体替换掉。
以上5步构成一代,一代一代往前进化,若干代停止。

