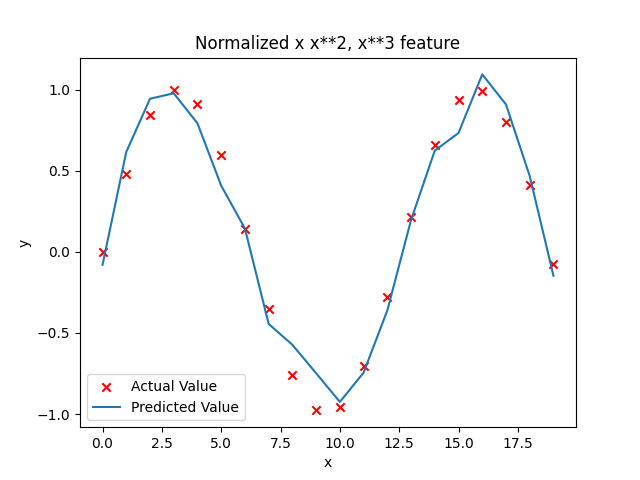
回归问题
线性回归就是多项式回归的一种特殊情况,在线性回归中只存在一次项,所以只能拟合直线,而多项式回归则存在高次项,可以拟合曲线。本文代码都是基于多项式回归的,所以w是一个向量,并且没有考虑多元函数的情况,只存在x和y两个变量
前言
机器学习中的线性回归是一种简单但强大的技术,其作用包括但不限于以下几个方面:
- 预测: 最常见的用途是用来预测目标变量的数值。通过学习输入特征和目标变量之间的线性关系,线性回归模型可以用来预测未知数据点的目标变量值。例如,根据房屋的面积、卧室数量等特征,预测房屋的售价。
- 关联分析: 可以用线性回归来分析输入特征与目标变量之间的关联程度。通过观察特征与目标变量之间的线性关系,可以识别出哪些特征对目标变量有显著影响,进而深入了解数据之间的关系。
- 异常检测: 通过观察模型的预测残差(实际值与预测值之间的差异),可以识别出可能是异常的数据点。这些异常点可能是数据采集或处理过程中的错误,或者是真实世界中的特殊情况,值得进一步调查。
- 特征工程: 线性回归可以用来评估特征的重要性和影响程度。基于模型的系数(权重),可以识别出哪些特征对目标变量的影响最大,从而指导特征选择和特征工程的过程。
- 解释性: 线性回归模型具有很强的解释性,模型的系数可以直观地解释特征对目标变量的影响程度。这使得线性回归在决策支持系统和业务解释性要求较高的场景中非常有用。
总的来说,线性回归在机器学习中扮演着重要的角色,是许多其他复杂模型的基础。它提供了一种简单而有效的方法来建模和预测数据,同时具有很强的解释性,使得其在实际应用中得到了广泛的应用。
成本函数
成本函数在回归问题中的作用是衡量模型预测值与真实值之间的差异,或者说衡量模型的预测误差。它是优化算法的核心,用于指导模型参数的更新,使得模型能够更好地拟合训练数据并得到更准确的预测结果。
具体来说,成本函数在回归问题中的作用包括以下几个方面:
评估模型性能: 成本函数提供了一个度量模型预测性能的指标。通过计算成本函数的值,可以了解模型对训练数据的拟合程度,以及模型的预测误差大小。成本函数的值越小,表示模型的预测结果与真实值越接近,模型性能越好。
优化模型参数: 成本函数是优化算法的目标函数,优化算法的目标是最小化成本函数的值。通过最小化成本函数,可以找到使模型预测误差最小化的参数值,从而得到更准确的模型。常见的优化算法包括梯度下降、随机梯度下降等,它们通过计算成本函数的梯度来指导参数的更新。
调整模型复杂度: 成本函数可以帮助调整模型的复杂度,以避免过拟合或欠拟合的问题。通过引入正则化项或调整模型的超参数,可以改变成本函数的形式,从而影响模型的学习过程和预测性能。
在回归问题中,常用的成本函数包括均方误差(Mean Squared Error,MSE)、均方根误差(Root Mean Squared Error,RMSE)、平均绝对误差(Mean Absolute Error,MAE)等。这些成本函数可以根据具体的问题和需求进行选择,用于评估模型的性能并指导模型的优化。
1 | def compute_cost(x, y, w, b): |
计算梯度
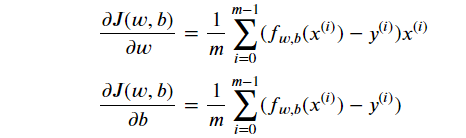
1 | def compute_gradient(x, y, w, b): |
标准化和归一化
标准化(Normalization)和归一化(Standardization)是数据预处理中常用的两种技术,它们的作用不同,适用于不同的情况:
标准化(Standardization):
- 作用: 标准化的主要作用是使数据的分布符合标准正态分布(均值为0,标准差为1)。通过减去特征的均值,然后除以特征的标准差,可以将数据的均值调整为0,标准差调整为1。
- 优点: 标准化不会改变数据的原始分布形状,适用于大部分机器学习算法,特别是那些对数据分布敏感的算法,如支持向量机(SVM)和k近邻(KNN)等。
- 适用情况: 当特征的数值范围差异较大,或者特征的分布不符合标准正态分布时,可以考虑使用标准化。
归一化(Normalization):
- 作用: 归一化的主要作用是将特征缩放到一个指定的范围内,通常是[0, 1]或[-1, 1]。通过对每个特征的数值进行线性变换,使其落在指定的范围内。
- 优点: 归一化可以消除特征之间的量纲差异,使得不同特征具有相同的重要性。它也有助于加速模型的收敛速度,并提高模型的性能。
- 适用情况: 当特征的数值范围差异较大,或者特征的数值范围不重要,但需要保证特征具有相同的重要性时,可以考虑使用归一化。
总的来说,标准化和归一化是常用的数据预处理技术,可以帮助提高模型的性能和稳定性。选择使用哪种技术取决于数据的特点和机器学习算法的需求,需要根据具体情况进行选择。
1 | def zscore_normalize_features(X): |
代码
1 | import numpy as np |
运行结果